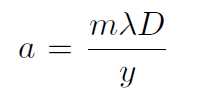UG Physics Laboratory
Department of Physics , LNMIIT Jaipur
UG Physics Laboratory
Department of Physics , LNMIIT Jaipur
1. To understand what is meant by Fraunhoffer diffraction.
2. To observe single slit diffraction patterns and plot the intensity profile of the pattern.
3. Determine slit width from the diffraction formula.
Diffraction is the wave phenomenon which describes the deviation from straight line propagation of a wave when it encounters an obstruction. In the case of light waves both opaque and transparent obstacles cause this effect which results in shadow patterns on a screen which are quite different from those expected if light travelled only in straight lines.
There are basically two categories of diffraction effects. The first is Fraunhoffer diffraction, which occurs when the waves incident on the slit and the screen (detector) are plane waves. This diffraction is produced when both the light source and screen are effectively at an infinite distance from the given obstacle. Fresnel diffraction is the second type and refers to diffraction produced when either the source or screen or both are at finite distances from the obstacle.
We can observe Fraunhoffer diffraction experimentally by using a collimated light source and (i) placing the viewing screen at the focal plane of a convex lens located behind the obstacle or (ii) by placing the screen at a large distance from the obstacle. The schematic of a single slit diffraction apparatus is shown in Fig. 10.1.
In this experiment we concentrate on Fraunhoffer diffraction patterns although you can observe the different patterns produced by Fresnel diffraction by placing the viewing screen close to the diffraction slit used.
Fig. 10.1 shows a plane wave of wavelength λ incident on a slit width a. The diffraction pattern, intensity versus y is plotted in the figure. Wave theory predicts that the Fraunhoffer diffraction pattern intensity due to a rectangular slit will be of the form
(10.1)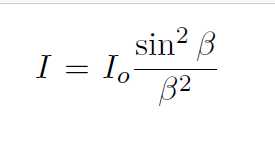
where β = (ka sin θ)/2, k = 2π/λ, a = slit width and θ = angle formed by the light ray with respect to the system central axis. The minima in the diffraction pattern occurs when I(θ) = 0. This condition requires that
(10.2)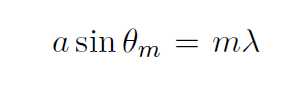
where, m is the order number in diffraction pattern and θm is angle measured with respect to system central axis to the mth order minima. The shape of this pattern is shown in
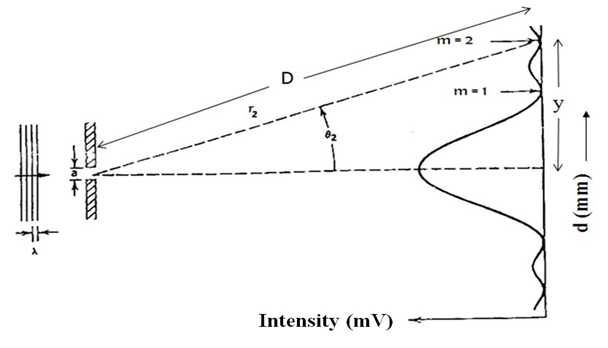
Figure 10.1: The Fraunhoffer diffraction pattern of a single slit.
Fig. 10.1. If θm is small, then
(10.3)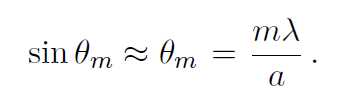
Further from geometry we have
(10.4)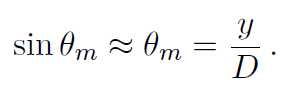
where y = the distance between central maxima to the mth order minima point and D = distance between slit and photo diode (observed form instrument). Combining Eqs. 10.3 and 10.4, the slit width can be calculated as
(10.5)
Digital Multi-meter (DMM), He-Ne laser source, sliding detector (photocell), optical rail and mounts.
1. Let the laser warm up for at least fifteen minutes before starting the experiment.
2. Position the laser at one end of the bench and align the beam so that it travels parallel to and along the central axis of the bench all along its length.
3. Let the beam pass through a beam expander. Adjust the slit position until the laser beam is incident on the full width of the slit.
Figure 10.2: Experimental setup for single slit diffraction pattern
4. Attach the viewing screen to a component carrier and position it at the end of the bench furthest from the laser.
5. Observe the diffraction pattern on the screen. Adjust the screen position if necessary to obtain image clarity. Sketch the pattern observed for two different slit widths. What is the effect of varying the slit width?
6. Now replace the screen with the sliding detector. Beware that the smallest division on the sliding detector is 0.01 cm, and the detector can be moved over a distance of 4 cm. Check that the un-obstructed laser beam is at the proper level to be incident on the detector central slit-adjust if necessary.
7. Adjust the position of the slit along the optical bench until the central (principal) maximum and the first subsidiary maxima of the single slit diffraction pattern are fully extended along the direction of travel of the detector–obviously the pattern gets wider as the slit is moved closer to the laser and hence further away from the detector.
8. Form a clear diffraction pattern and SLOWLY scan the pattern from the central maxima to first maxima on the one side with the sliding detector for every 25 divisions of the circular scale.
9. Plot intensity versus position. How do your results agree with theoretical predictions?
10. Calculate the slit width using the diffraction Eq 10.5.
The calculated slit width from the diffraction pattern a = ....... mm.
1. Never look directly into the laser beam and take care to avoid reflections entering your eyes.
2. Do not disturb the setup once the diffraction pattern has been obtained.
3. Do not use the backlight of the multimeter. This would drain the battery of the multimeter.
4. Avoid stray light falling on the photo detector while measuring the instensity of light.
Copyright © 2018- Department of Physics, LNMIIT. All Rights Reserved.
Handcrafted with by LUSIP 2018 Team1
Theory
Procedure
Video
Resources
Viva Voce
