LNMIIT UG Physics Lab

Aim :

1. To study the flux and emf in the coil as a function of time

2. To study the maximum emf and total flux as a function of the velocity of the magnet.

3. To demonstrate damping due to induced current

Theory :

Faraday’s law of electromagnetic induction tells us that a change in magnetic flux gives rise to an induced emf " given by

(8.1)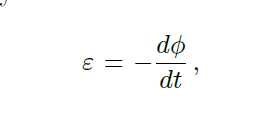

where φ is the magnetic flux. A simple apparatus has been designed, whose schematic

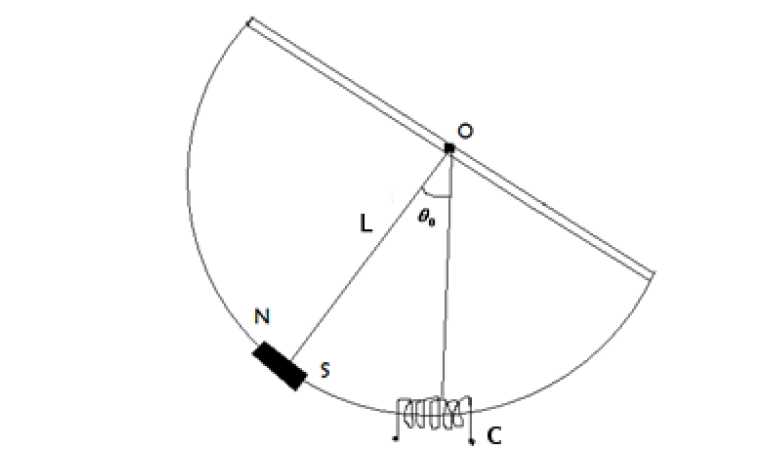
Figure 8.1: Schematic of the coil moving in and out of the magnetic field.

diagram is shown in Fig. (8.1), enables us to change θ at different rates through a coil of suitable area of cross-section. A rigid semicircular frame of aluminium is pivoted at the centre of the semicircle. The whole frame can oscillate freely in its own plane, about a horizontal axis passing through its centre. A bar magnet can be mounted at the centre of the arc and the arc passes through a coil C.

It is very instructive to study the emf, induced in the coil as the magnet passes through the coil while oscillating. In this experiment we will use a computer to monitor emf induced as a function of time.

The rate of change of flux through the coil is essentially proportional to the velocity of the magnet, as it passes through the coil. Choosing different amplitudes of oscillations can vary the velocity.

If I is the moment of inertia of the oscillatory system and ω is the angular velocity of the magnet, then the kinetic energy of the system is Iω^2/2 and potential energy can be represented by MgL(1 − cosθ) at any instant of time, where L is the effective length of the corresponding simple pendulum. If θo is the maximum angular amplitude and ωmax is the maximum value of angular velocity, then

(8.2)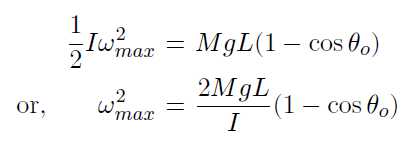

The motion can be regarded approximately as simple harmonic and its time period is given by

(8.3)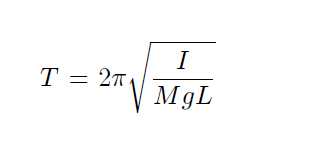

From Eq. (8.2) and (8.3), we get.

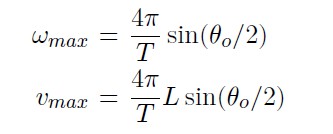
where vmax is the maximum linear velocity associated with ωmax. Angular amplitude θo is directly measured from the instrument. Velocity is computed by measuring T and θo.

Apparatus Required :

Faraday setup, diode, capacitor, breadboard, connecting wire, CRO etc.

Procedure :

1. Charging of capacitor to obtain εmax The induced emf can be measured by using a simple circuit as shown in Fig. 8.2. The induced emf in the coil charges a capacitor C, through a resistance R and a diode D and the voltage developed across C is measured by voltmeter V . The diode current can flow only if the voltage at A is greater than B. Thus once a capacitor attains a voltage ", current can flow through the capacitor only if the induced emf is greater than ". If the time constant RC is not small compared to the time taken for the magnet to cross the coil, the capacitor does not get fully charged in AC signal oscillation. It may take several oscillations to do so.

Connect a resistor, diode and a capacitor given to you in series with the coil. Observe the signal across resistor, diode and the capacitor as a function of time

Calculate vmax using Eq. (8.5) and plot a graph between "max vs vmax. "max is the maximum potential obtained in the CRO.

2. Induced emf as a function of velocityYou can use the computer interface provided to measure the voltage as a function of time. The instructor will explain you how to use the software.

Figure 8.2: Circuit diagram for charging of a capacitor

Ensure that the support for the apparatus is vertical by adjusting levelling screws. Adjust the weights W1 and W2 mounted on the horizontal bar to make zero of the scale as the mean position. Centre of the magnet must be inside the coil.
Ensure that the support for the apparatus is vertical by adjusting levelling screws. Adjust the weights W1 and W2 mounted on the horizontal bar to make zero of the scale as the mean position. Centre of the magnet must be inside the coil.
Plot of t vs φ(t): Record one or two oscillations. Focus on only one of them by using magnification button. Use the integration feature of the software to obtain flux φ as a function of time. You can integrate only half of the pulse, since the pulse is highly symmetric. Plot this on a graph paper for the complete pulse.
vmax dependence of slope of "(t) at mean position and φ: The emf induced in the coil can be written as

Note that when the magnet is at its mean position, then ω = ωmax or velocity is at its maximum since Vmax = ωmax R. However, dφ/dθ = 0 at that point. Hence emf will go through a zero corresponding to the mean position. Also note that

Hence a plot of the slope of ε(t) at the zero, corresponding to the mean position against v^2 max would be linear. The proportionality constant depends only on the geometry of the coil and the magnet. For calculating φ use “Show integral" mode as before.

3. Electromagnetic damping in an oscillating system We observe that the successive oscillations are not of the same amplitude. This is due to damping. Possible sources are: (i) air resistance, (ii) friction at the point of suspension, and (iii) induced emf (Lenz’s law).

The system (for small ) and for damping proportional to velocity would satisfy the equation.

(8.8)

where I is moment of inertia about origin, k is damping coefficient and λ0 is restoring couple (Mgl0), if treated as a simple pendulum of length 1.

The amplitude would exponentially decay only if k is a constant and damping term depends linearly in velocity. Record a large number of oscillations starting from initial amplitude of 300 to study the damping behaviour in the absence of induced current in the coil. The plot seen on the screen may not be correct representation of data since the number of points to be plotted is too large. Therefore divide the time axis to approximately 8 to 10 zones and take data after magnifying 1 pulse from each zone. Plot ωmax and (dω/dt)(vmax) as a function of time or number of oscillations. From your data calculate Q of this oscillator using A = Aoert/2 and Q = ωo/r.

Now, connect a resistor of about 220 (the coil resistance is around 900) in series with the coil and record voltage dropped across the resistor as a function of time (for large number of oscillations as in the previous case). Repeat analysis of data as above.

4. Useful features of the software measure:

It is easy to use the software given to you. Take a few minutes to summarize yourself with it before going to the detailed experiments. All you have to do is to click the required icon given at the top. Some of the important ones are as follows:

ARROW: In this mode simply point the cursor at the required point to obtain values of the coordinates.

MARK: Use this mark a portion of the curve. The x-coordinate of the mark portion are shown on the bottom. The marked portion is highlighted in a different colour.

SURVEY: You can adjust the left bottom and right top coordinates of the cursor box to obtain coordinates and their differences in this mode. You can use this to calculate slopes around a point.

SHOW INTEGRAL: Mark the portion of the curve for which you need to calculate the integral and then click this icon to obtain the value. If you need to start from the origin, each time, take the cursor out of the plotting area and drag it across the origin to ensure that starting point is the same.

SLOPE: Mark the required portion of the curve for which you need the slope and then click this icon to get slope. However, we recommend use of survey mode to get slope more accurate.

Electromagnetic induction

Aim :

Theory :

Apparatus Required :

Procedure :

Observations :

Result :

VIDEO

RESOURCES

VIVA VOCE