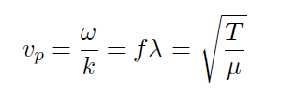LNMIIT UG Physics Lab

Aim :

1. Study wavelength (λ) as function of frequency (ν) and to find out the phase velocity vp of a traveling wave in a string.

2. To measure linear mass density μ of the string.

Theory :

A wave is an oscillation which propagates itself in space and time and usually periodically through matter and space. One can differentiate between transverse and longitudinal waves. In the case of transverse waves, the oscillation is perpendicular to the direction of the propagation of the wave. In the case of longitudinal waves, the oscillation and the propagation are in the same direction.

Our goal here is to find out the phase velocity of a wave. In order to calculate the velocity we need to know the frequency and the wavelength. Frequency is generated by function generator and is an independent variable here. So our main task is to calculate wavelength of the wave. Here in this experiment we calculate wavelength using a novel technique

A standing wave is created by reflecting the wave from its opposite end. The distance between the nodes is measured and thus the wavelength is calculated. A typical harmonic wave can be represented as,

(9.1)

y = Asin(kx − ωt)

where,

y is the displacement of the particle from its mean position at a position x and at a time t.

A is the amplitude of the oscilation.

k is called the wave number and is related to the wavelength λ by the relation k = 2π/λ.

ω is called the angular frequency (measuered in radians per meter) and is 2π times the frequency.

Now consider two transverse waves having same amplitude, frequency, and wavelength but travelling in opposite directions in the same medium

y1 = Asin(kx − ωt)

(9.2)

and y2 = Asin(kx + ωt)

where y1 represents a wave traveling in the +x direction and y2 represents a wave traveling in −x direction. Adding these two functions gives the resultant wave function y

(9.3)

y = y1 + y2

(9.3)

y= Asin(kx − ωt) + Asin(kx + ωt)

(9.4)

y = 2Asin(kx) cos(ωt)

This represents a wave function of standing waves. The speed of a wave on a string which is under tension T and having a mass per unit length μ is given by

(9.5)

Apparatus Required :

Function generator, amplifier, mechanical oscillator, rubber rope, measuring tape, support rod, support base, and weights.

Experimental setup

A schematic diagram of the experimental setup is shown in Fig. 9.1 while Fig. 9.2 shows the various intruments of the experiment.

Figure 9.1: Schematic of standing wave generation.

Figure 9.2: Experimental setup Observation

Observations :

For a given setup, record

1. Frequency from the function generator (10Hz − 25Hz).

2. Tension from the weight attached to the rope through the pulley.

3. Wavelength from the position of the nodes.

For constant mass m = ......... kg

For varying mass

Calculations :

1. Plot the 1/λ vs frequency graph. From this graph, the phase velocity vp should be determined. Keep the tension in the string constant i.e. mass is constant.

The phase velocity vp of the rope waves, which depends on the tensile stress (T) on the rope, is to be measured for a given frequency. Plot v^2p vs T and hence find the mass/unit length of the string using Eq. (9.5).

Result :

1. Phase velocity (for constant mass) vp = ......

2. Mass per unit length (for constant frequency) μ = .......

VIVA VOCE

-Check Yourself-

1. For a given harmonic, the wavelength λ is where L is the length of the stretch string and n is the number of segments in the string

λ =2n/L
λ =2L/n
λ =2nL
λ =L/2n

2. The velocity of a wave traveling in a string is also dependent on

Tension
linear mass density
length
a & b both

3. If the frequency is varied while the tension and length are held constant, a plot of frequency , f , vs. number of segments, n , will give a

Straight line
Parabola
circle
increasing curve

4. The velocity of any wave is given by

λf
2Lf/n
λ/f
a & b both

5. The speed of a wave on a string which is under tension T and having a mass per unit length μ is given by

√𝞵T
√^𝞵⁄_T
√^T⁄_μ
^𝞵⁄_T

6. The velocity of mechanical wave depends on

inertia of the medium
elasticity of the medium
elasticity and inertia of the medium
none

7. y1 represents a wave traveling in the one direction and y2 represents a wave traveling in opposite direction. Adding these two functions gives the resultant wave function y which have

Only sin function
Only cos function
Both sin and cos function
Is a constant function

8. k which is wave number, is given by

2πf
2πλ
2πL
None

Mechanical waves